$$\require{extpfeil}\Newextarrow{\xRightarrow}{5,5}{0x21D2}$$ Laser scanning using a laser pointing device and a camera

The method is (usually) based on triangulation. This means that a triangle has to be formed, having the camera, the laser device and an unknown point as vertices. Using the law of sines, one can calculate the distance from the unknown point, thus resolving the 3D geometric problem. Here is how this can be done:

Fig. 1. The process of triangulation for an unknown point in 3D space

The baseline distance between the camera and laser diode is denoted by \(d\), while \(\phi\) is the angle of the camera and \(\theta\) the angle of the laser both with the axis vertical to the line that connects them. In total, the variables that are the known parameters of this arrangement are (for a pinhole camera model):
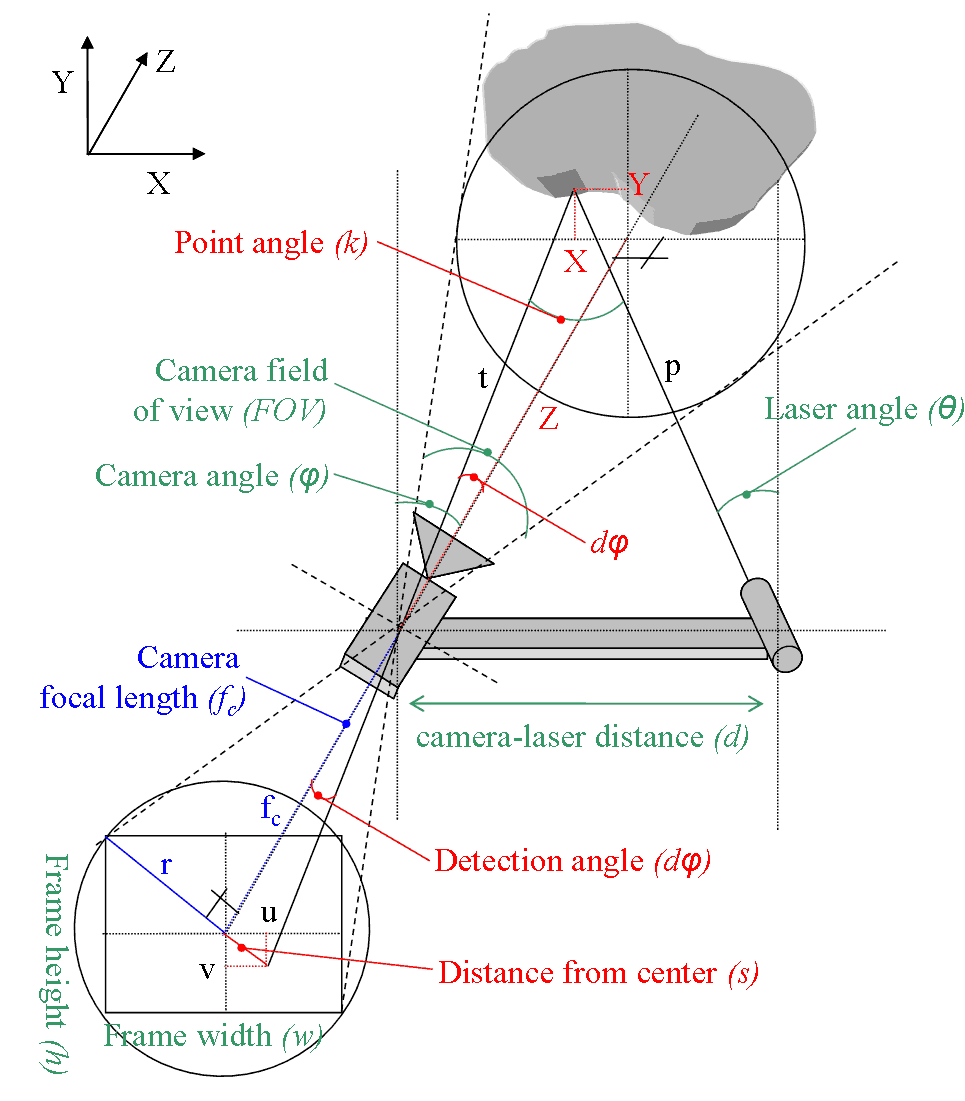
$$ \left.\begin{array}{l} \displaystyle \text{tan}\left(\frac {\text{FOV}} 2\right) = \frac r f_c \\ \displaystyle (2r)^2 = w^2 + h^2 \end{array} \right\} \Rightarrow \displaystyle f_c = \frac {\displaystyle {\frac {\sqrt{w^2+h^2}} 2}} {\displaystyle {\text{tan}\left(\frac {\text{FOV}} 2\right)}} \Rightarrow \displaystyle f_c = \frac {\sqrt{w^2+h^2}}{\displaystyle 2\cdot{\text{tan}\left(\frac {\text{FOV}} 2\right)}} $$ (1)


Triangulation is based on the law of sines, which states that if the sides of an arbitrary triangle are \(a,b,c\) and the angles opposite those sides are \(A,B,C\):
$$ \frac{\displaystyle a}{\displaystyle \text{sin}(A)} = \frac{\displaystyle b}{\displaystyle \text{sin}(B)} = \frac{\displaystyle c}{\displaystyle \text{sin}(C)} = 2R $$ (2)

where \(R\) is the radius of the triangle’s circumcircle.
In the described case, equation (2) becomes:
$$ \frac{\displaystyle d}{\displaystyle \text{sin}(k)} = \frac{\displaystyle p}{\displaystyle \text{sin}\left(\frac{\pi}{2}-\phi+d\phi\right)} = \frac{\displaystyle t}{\displaystyle \text{sin}\left(\frac{\pi}{2}-\theta \right)} = 2R $$ (3)


In this topology the problem is a typical geometric problem that can be easily solved, as:
$$ \begin{array}{l} k+\left(\frac{\displaystyle \pi}{\displaystyle 2}-\phi+d\phi\right)+\left(\frac{\displaystyle \pi}{\displaystyle 2}-\theta\right) = \pi \Rightarrow \\ k = \pi-\left(\frac{\displaystyle \pi}{\displaystyle 2}-\phi+d\phi\right)-\left(\frac{\displaystyle \pi}{\displaystyle 2}-\theta\right)=\phi+\theta-d\phi \end{array} $$ (4)

and, as of this, the unknown distance from the camera is:
$$ \frac{\displaystyle d}{\displaystyle \text{sin}k} = \frac{\displaystyle t}{\text{sin}\left(\frac{\displaystyle \pi}{\displaystyle 2}-\theta\right)} \Rightarrow t = d \frac{\text{sin}\left(\frac{\displaystyle \pi}{\displaystyle 2}-\theta\right)}{\displaystyle \text{sin}(\phi+\theta-d\phi)} $$ (5)


The only unknown variable here is the angle \(d\phi\), which can easily be estimated trigonometrically:
$$ \begin{array}{l} \text{tan}(d\phi) = \frac{\displaystyle s}{\displaystyle f_c} \Rightarrow d\phi = \text{arctan}\left(\frac{\displaystyle s}{\displaystyle f_c}\right) \Rightarrow \\ d\phi = \text{arctan}\left(\frac{\displaystyle \sqrt{u^2+v^2}}{\displaystyle f_c}\right) \\ \text{or} \\ d\phi = \text{arctan}\left(2\frac{\displaystyle \sqrt{u^2+v^2}}{\displaystyle \sqrt{w^2+h^2}}\text{tan}\left(\frac{\displaystyle \text{FOV}}{\displaystyle 2}\right)\right) \end{array} $$ (6)


In practice, it is more convenient to estimate the \(X,Y,Z\) coordinates of the detected point instead of its distance from the camera \(t\). This can be achieved if instead of working with the distance \(s\) we estimate angles in \(X\) and \(Y\) axis separately. The notion is depicted graphically in Fig. 2, where the detection angle \(d\phi\) is represented by two angles that are relative to one axis, i.e. \(d\phi_X\) for \(X\) and \(d\phi_Y\) for \(Y\).

Fig 2. A more practical approach to the estimation of the unknown coordinates of a detected point

The estimation of these angles is equivalent to the estimation of \(d\phi\) in (6). The final equations are:
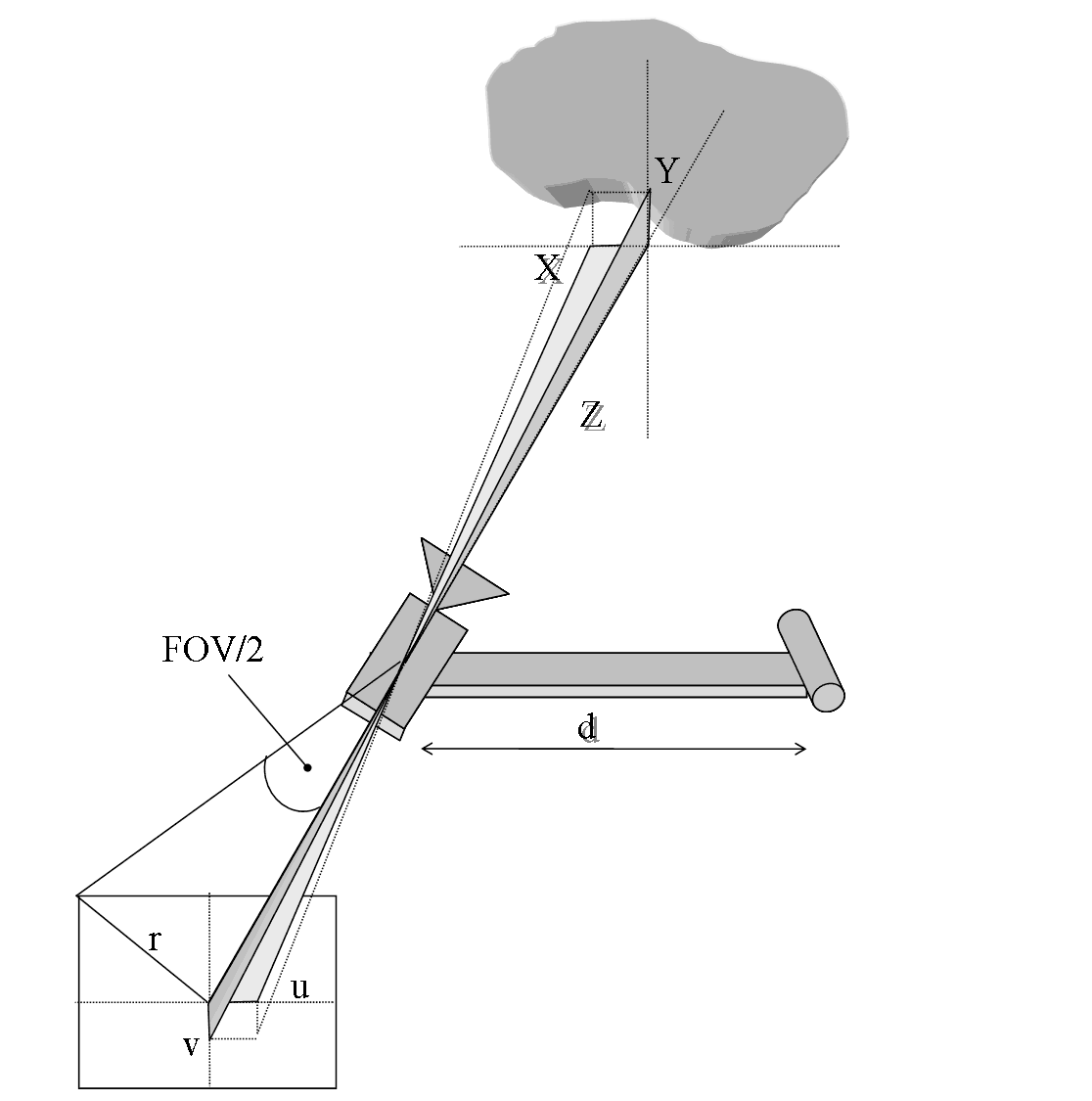
$$ d\phi_u = \text{arctan}\left( \frac{\displaystyle u}{\displaystyle r} \text{tan} \left( \frac{\displaystyle \text{FOV}}{\displaystyle 2} \right) \right) \\ d\phi_v = \text{arctan}\left( \frac{\displaystyle v}{\displaystyle r} \text{tan} \left( \frac{\displaystyle \text{FOV}}{\displaystyle 2} \right) \right) $$ (7)
Having in mind that 
$$ f_c = \frac{\displaystyle r}{\displaystyle \text{tan}\left(\frac{\displaystyle \text{FOV}}{\displaystyle 2}\right)} $$ (8)
We get 
$$ d\phi_u = \text{arctan}\left( \frac{\displaystyle u}{\displaystyle f_c} \right) \\ d\phi_v = \text{arctan}\left( \frac{\displaystyle v}{\displaystyle f_c} \right) $$ (9)
Thus since angles in the object side are equal to the angles in the image side 
$$ d\phi_X = d\phi_u \Rightarrow \text{arctan}\left(\frac{\displaystyle X}{\displaystyle Z}\right) = \text{arctan}\left( \frac{\displaystyle u}{\displaystyle f_c} \right) \xRightarrow[\text{of generality}]{\text{without loss}} X = Z \frac{\displaystyle u}{\displaystyle f_c} \\ d\phi_Y = d\phi_v \Rightarrow \text{arctan}\left(\frac{\displaystyle Y}{\displaystyle Z}\right) = \text{arctan}\left( \frac{\displaystyle v}{\displaystyle f_c} \right) \xRightarrow[\text{of generality}]{\text{without loss}} Y = Z \frac{\displaystyle v}{\displaystyle f_c} $$ (10)
From the geometry of the problem and equation (5) we have 
$$ Z = \text{cos}(d\phi) \cdot t = d \frac{\displaystyle \text{cos}(d\phi)\, \text{sin}\left(\frac{\displaystyle \pi}{\displaystyle 2}-\theta\right)}{\displaystyle \text{sin}(\phi+\theta-d\phi)} \Rightarrow Z = d \frac{\displaystyle \text{cos}(d\phi)\, \text{cos}(\theta)}{\displaystyle \text{sin}(\phi+\theta-d\phi)} $$ (11)


Overall, we may use equation (6) to get the \(d\phi\) angle using all known parameters, then apply it to equation (11) to estimate the \(Z\) coordinate, and finally use equations (10) to get the remaining \(X,Y\) coordinates.

A practical example of the triangulation process
In the following images, a portion of a scanning sequence is shown (Fig. 3). The laser device projects a line on the objects of interest and an image is captured in the camera at every time interval. The detected laser light is then processed pixel-by-pixel in order to deduce the geometry of the objects (Fig. 4).

1 2 3
4 5 6

Fig 3. Six (1 to 6) consecutive images (with step two images) from the test data set. The green line is the laser projected on the object.


Fig 4. The result of the digitization process (point cloud) at different time intervals.


2006, George P. Pavlidis, CETI/ATHENA
Return to calling page...