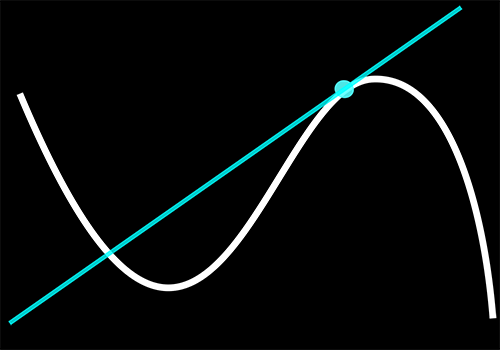
Formally stated, the derivative of a function of the form
$latex \displaystyle f = k \cdot u^a \cdot v^b \cdots &s=2$
with k a constant and with respect to an independent variable x, is simply,
$latex \displaystyle \frac{\mathrm{d}f}{\mathrm{d}x} = f \cdot \left [ a \frac{\dot{u}}{u} + b \frac{\dot{v}}{v} + \cdots \right ] &s=2$
I find this to be extremely handy in all cases. Consider the simple case in which,
$latex \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \left ( 1+3x \right ) ^2 &s=1$
$latex \displaystyle \text{here } f = u^a = \left ( 1+3x \right ) ^2 \Rightarrow u=(1+3x), \; a=2, \; k=1 &s=1$
$latex \displaystyle \text{using the method above } \frac{\mathrm{d}f}{\mathrm{d}x} = f \cdot a \frac{\dot{u}}{u} &s=1$
$latex \displaystyle \text{thus } \frac{\mathrm{d}f}{\mathrm{d}x} = (1+3x)^2 \cdot 2 \frac{3}{(1+3x)} = 6(1+3x) &s=1$
In the same way,
$latex \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} (3x^2+2x) = 6x+2 &s=1$
In a more complex example,
$latex \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} 6(1+2x^2)(x^3-x)^2 = \\ = 6(1+2x^2)(x^3-x)^2 \cdot \left [ \frac{4x}{1+2x^2} + 2 \frac{3x^2-1}{x^3-1} \right ] &s=1$
In an even more complex example,
$latex \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \frac{4}{\sqrt{x+3x^2} \cdot (2x)^{5/2}} = \\ = \frac{4}{\sqrt{x+3x^2} \cdot (2x)^{5/2}} \cdot \left [ -\frac{1}{2} \frac{1+6x}{x+3x^2} -\frac{5}{2} \frac{2}{2x} \right ] &s=1$
How about this one?
$latex \displaystyle \frac{\mathrm{d}}{\mathrm{d}x} \left [ 6(1+2x^2)(x^3-x)^2 + \frac{4}{\sqrt{x+3x^2} \cdot (2x)^{5/2}} \right ] = \\ = 6(1+2x^2)(x^3-x)^2 \cdot \left [ \frac{4x}{1+2x^2} + 2 \frac{3x^2-1}{x^3-1} \right ] + \\ + \frac{4}{\sqrt{x+3x^2} \cdot (2x)^{5/2}} \cdot \left [ -\frac{1}{2} \frac{1+6x}{x+3x^2} -\frac{5}{2} \frac{2}{2x} \right ] &s=1$
Unbelievably powerful!