Differentiation cheat sheet

sepdek October 13, 2016

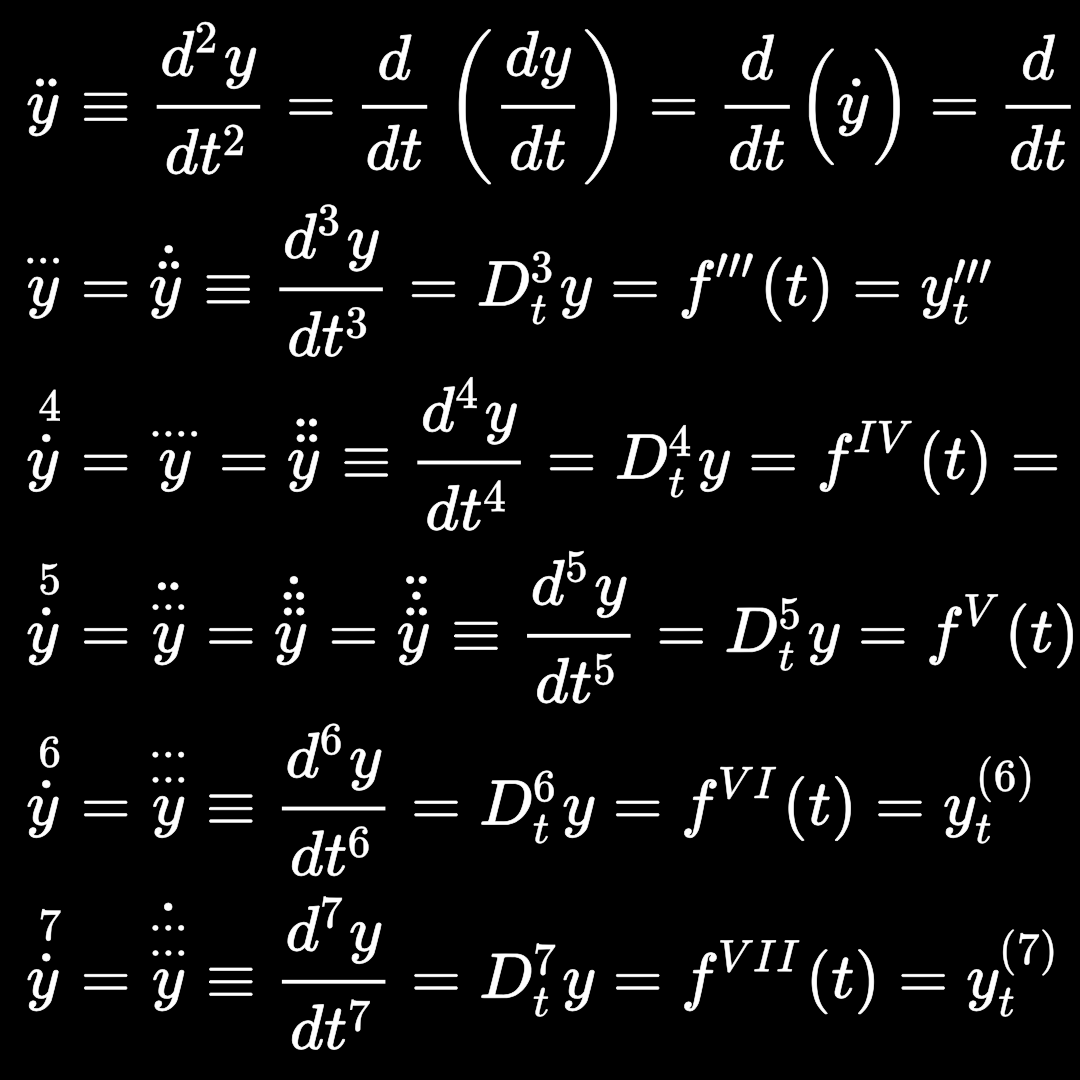
This post serves as a cheat sheet for differentiation. It just includes the most basic of the rules to be remembered when computing derivatives. First a little reminder on the notation being used in differentiation.

Leibniz’s notation for the first derivative of a function f(x) is
$\displaystyle \frac{\mathrm{d}f(x)}{\mathrm{d}x}$

Newton’s notation for the first derivative of a function f(x) is
$\displaystyle \dot{f}$

Lagrange’s notation for the first derivative of a function f(x) is
$\displaystyle f^\prime(x)$

Euler’s notation for the first derivative of a function f(x) is
$\displaystyle D_xf(x)$

These notations are being used interchangeably and each seems to be more appropriate for some special cases, in which the mathematical expression becomes ‘clearer’ or ‘beautiful’.

In the following differentiation cheat sheet I am going to use Newton’s notation.

Constant	$\displaystyle f(x) = c \Rightarrow \dot{f} = 0$
Constant times a function	$\displaystyle f(x) = c \cdot u(x) \Rightarrow \dot{f} = c \cdot \dot{u}$
Power	$\displaystyle f(x) = x^n \Rightarrow \dot{f} = nx^{n-1}$
Constant times a power	$\displaystyle f(x) = c \cdot x^n \Rightarrow \dot{f} = cnx^{n-1}$
Sum of functions	$\displaystyle f(x) = u(x)+v(x) \Rightarrow \dot{f} = \dot{u} + \dot{v}$
Product of functions	$\displaystyle f(x) = u(x) \cdot v(x) \Rightarrow \dot{f} = v \dot{u} + u \dot{v}$
Quotient of functions	$\displaystyle f(x) = \frac{u(x)}{v(x)} \Rightarrow \dot{f} = \frac{v \dot{u}-u\dot{v}}{v^2}$
Chain rule	$\displaystyle f(x) = u(v(x)) \Rightarrow \dot{f} = \dot{v} \cdot \dot{u}(v)$
Chain rule special	$\displaystyle f(x) = [u(x)]^n \Rightarrow \dot{f} = n[u(x)]^{n-1}\dot{u}$
Exponent	$\displaystyle f(x) = e^{u(x)} \Rightarrow \dot{f} = \dot{u}e^{u(x)}$
Exponent special	$\displaystyle f(x) = e^x \Rightarrow \dot{f} = f(x) = e^x$
Logarithic	$\displaystyle f(x) = \log{u(x)} \Rightarrow \dot{f} = \frac{\dot{u}}{u}$
Logarithmic special	$\displaystyle f(x) = \log{x} \Rightarrow \dot{f} = \frac{1}{x}$

Let’s try to derive the extremely powerful differentiation method described in a previous post.

In that post it was stated that the derivative of a function of the form
$\displaystyle f = k \cdot u^a \cdot v^b \cdots$
with k a constant and with respect to an independent variable x, is simply,
$\displaystyle \dot{f} = f \cdot \left [ a \frac{\dot{u}}{u} + b \frac{\dot{v}}{v} + \cdots \right ]$

Let us consider the simplest case, in which
$\displaystyle f = k \cdot u^a \cdot v^b$

with a little bit of mixing (primarily) of the product rule and the chain rule we get,
$\displaystyle \dot{f} = k (v^b \dot{u^a} + u^a \dot{v^b}) \\ = k (v^b a u^{a-1}\dot{u} + u^a b v^{b-1}\dot{v})$

but is is easy to see that from the original function,
$\displaystyle f = k \cdot u^a \cdot v^b \Rightarrow f = k \cdot (u^{a-1}u) \cdot v^b \Rightarrow v^b u^{a-1} = \frac{f}{ku}$

and similarly,
$\displaystyle f = k \cdot u^a \cdot v^b \Rightarrow f = k \cdot u^a \cdot (v^{b-1}v) \Rightarrow u^a v^{b-1} = \frac{f}{kv}$

Why do we need these two? simply because they showed up in the previous expression, in which we got stuck (momentarily), thus,
$\displaystyle \dot{f} = k \left[ a \frac{f}{ku} \dot{u} + b \frac{f}{kv} \dot{v} \right] = k \frac{f}{k} \left[ a \frac{\dot{u}}{u} + b \frac{\dot{v}}{v} \right] = f \left[ a \frac{\dot{u}}{u} + b \frac{\dot{v}}{v} \right]$
◻ QED

Discussion

comments

@sepdek's

More or less about me and everything that I learn, or hear, or think and find interesting to note.

Differentiation cheat sheet

Related

Discussion

Leave a CommentCancel reply

Subscribe to Blog via Email

Topics in this blog

Stay up to date

Athena Research Centre, Xanthi’s Branch

Athena Research Centre

CAA Greece

Share this:

Related

Discussion

Leave a CommentCancel reply