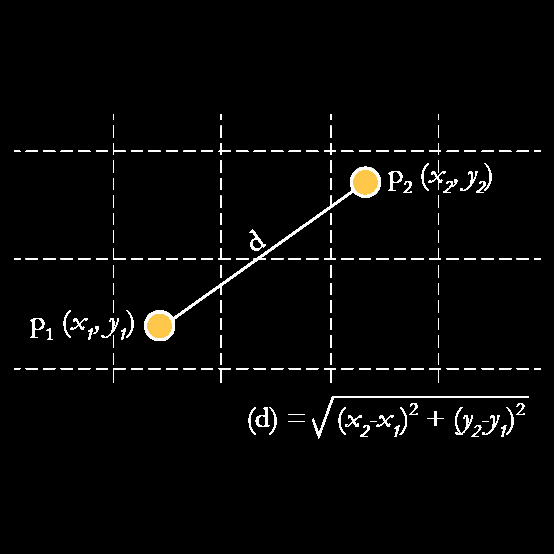
In order to be a measure (distance) d must:
In order to be a metric (distance) d has to be a measure and:
…and here is the cheat sheet:


In order to be a measure (distance) d must:
In order to be a metric (distance) d has to be a measure and:
…and here is the cheat sheet:
